中学3年生の数学では、「円の性質」という単元を学習します。
そこでこの記事では、この単元が苦手という中学生やそして中学生に勉強を教える親御さんのために抑えておくべき重要なポイントをわかりやすくまとめたので参考にしてください。
円の性質は「円周角の定理」が重要
円の性質で最も重要なのは、円周角の定理です。
円周角の定理をを理解するために、最初に「円周角」と「中心角」の意味をしっかりと覚える必要があります。
円周角とは
円周角とは、ユークリッド幾何学においてある円周上の一点から、この点を含まない円周上の異なる二点へそれぞれ線分を引くとき、その二つの線分のなす角のことです。 しかし、これでは理解できない人が大半でしょう。 噛み砕いて説明すると、「円周上の1点」と、それ以外の円周上からとった2つの点を、線分でむすんだときにできる角度のことを、円周角と読んでいます。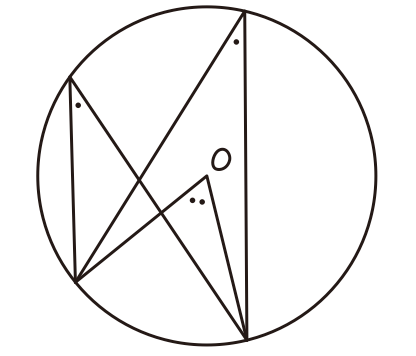
たとえば、円Oがあったとします。
円周上の点をA・B・Pとした場合、∠APBを弧ABに対する円周角といいます。
中心角とは
中心角とは、弧の両端を通る2つの半径の作る角です。 たとえば、下の円Oだったら、∠AOBが弧ABに対する「中心角」となります。円周角の定理を解説
円周角と中心角がわかったところで、円周角の定理の説明をしていきます。 円周角の定理とは円周角と中心角について成り立つもので、以下の2点の性質があります。- 1つの弧に対する円周角の大きさは一定で等しい
- 1つの弧に対する円周角の大きさは，中心角の半分になる
1つの弧に対する円周角の大きさは一定で等しい
これは、円周角の性質を表しています。 同じ弧の円周角ならすべて等しいということですが、しっかり同じ弧であることに注意しましょう。1つの弧に対する円周角の大きさは，中心角の半分になる
これは、円周角と中心角の性質を表していま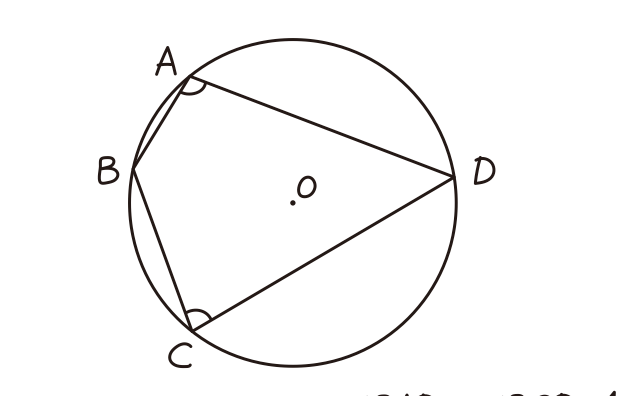す。
たとえば、このとき、円周角APBは中心角AOBの半分になります。
式であらわすと以下の通りです。
角APB = ½ 角AOB
これが、円周角の定理のうち、同じ弧に対する円周角と中心角の関係で、もし、円周角APBが「50°」だとしたら、中心角AOBは「100°」になります。
