【中3数学】「三平方の定理」の重要ポイントをピックアップし、勉強方法を紹介！

中学3年生の数学では、「三平方の定理」という単元を学習します。 そこでこの記事では、この単元が苦手という中学生やそして中学生に勉強を教える親御さんのために抑えておくべき重要なポイントをわかりやすくまとめたので参考にしてください。

三平方の定理とは

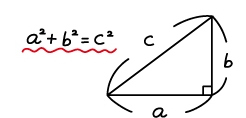三平方の定理は、ピタゴラスの定理とも言われ、直角三角形の3辺の長さに関する定理です。 2辺の長さをa，b，斜辺の長さをcとする直角三角形において成り立つ，「斜辺以外の2辺の長さをそれぞれ2乗して足すと、斜辺の長さの2乗に等しくなる」という定理です。

3辺の長さがa,b,cの直角三角形の場合、

a²+b²=c²

斜辺cの2乗は，他の辺a，bをそれぞれ2乗した数の和に等しいという定理となっているため。直角三角形では，2つの辺の長さがわかると，三平方の定理を使って他の1辺の長さが計算ができるのです。 また，三平方の定理の逆も成り立つことも理解しましょう。 3辺の長さがa，b，cの△ABCにおいて，a²+b²=c²が成り立つならば，△ABCは直角三角形であるということです。

三平方の定理を使う問題とは？

三平方の定理の利用法は「直角三角形の2つの辺の長さから、もう一つの辺の長さを求める」ということで、基本的な問題だと2辺がわかっていて残り1辺の長さを求めるという問題で使われます。 図形問題では頻出のため、覚えておく必要があります。 ただし高校入試レベルの問題となると、そのままの形で登場することは少なく、相似や合同などの他の図形的知識と組み合わされた、融合的な図形問題を解く場合の一つの手段として用いられます。 ですので、一見ここは三平方の定理を使う場面なのかどうか分かりにくいような問題がよく出てくるため、使い所を「見抜く」力が必要になってきます。

余談：ピタゴラスが定理を発見した逸話

「ピタゴラスは、サモス島のヘーラー神殿というところを散策していたときに、足元に敷き詰められた直角三角形のタイルを見て、この定理を思いついた」などと言われています。 この他にも逸話が知られているものの、この定理はピタゴラスが発見したかどうかは分からず、バビロニア数学のプリンプトン322や古代エジプトなどでもピタゴラス数については知られていたが、彼らが定理を発見していたかどうかは定かでは内容です。

三角定規の比率と角度を覚えよう

平方の定理の問題を解く上で、三角定規の直角三角形の2つの比と角度を覚えておくととても役に立ちます。 三角定規は以下の二つの直角三角形となっています。

• 30°，60°，90°の直角三角形で、辺の長さの比は、1：2:√3
• 45°，45°，90°の直角三角形で、辺の長さの比は、1：1：√2

つまり、30°，60°，90°の直角三角形の辺の長さの比は、1：2:√3であり、逆に辺の長さの比が1：2:√3の直角三角形の角度は30°，60°，90の3つということが成り立ちます。 また、同様に45°，45°，90°の直角三角形の辺の長さの比は、1：1：√2であり、逆に辺の長さの比が1：1：√2の直角三角形の角度は45°，45°，90°の3つということが成り立ちます。 これを覚えておくことですぐに解ける問題もあるので、必ず抑えておきましょう。

覚えると便利なピタゴラス数

整数だけで三平方の定理が成立する三辺の比のグループのことを、「ピタゴラス数」と呼ばれます 代表的なのが「3：4：5」で、この比率の長さの三角形は必ず直角三角形となっています。 この他にも以下のピタゴラス数があるので、覚えておくとすぐに解ける問題もあるので、余裕がある方は覚えましょう。

• 3:4:5
• 5:12:13
• 8:15:17
• 7:24:25

上記のピタゴラス数の一番右、一番大きい数字は斜辺に当たります。